引言：从离散到连续世界的跨越¶

基于上一节对于简单随机游走的介绍，这一节将进一步深化我们对随机过程的理解，从上一讲中介绍的简单、离散的模型，演进到能够更精确地描述物理现实的连续模型。这一过程将通过两个关键的推广来实现：

空间的连续化：我们将把随机游走模型从一个固定的、离散的晶格推广到连续的空间中。这一步将自然地引导我们从二项分布走向高斯分布，从而建立高斯随机游走（Gaussian Random Walk, GRW）模型。
时间的随机化：我们将打破“时间步”是固定且确定的这一限制，转而探讨事件在连续时间轴上随机发生的场景。这将引出统计物理和生物学中至关重要的泊松过程（Poisson Process）。

通过放宽对空间和时间的严格约束，我们能够构建出更具普适性和应用价值的理论框架，为理解从分子马达到宏观扩散等一系列现象奠定基础。

为了梳理本讲座至今所学的模型，下表对它们的关键特性进行了总结和对比：

特性	简单随机游走 (SRW)	高斯随机游走 (GRW)	泊松过程 (Poisson Process)
时间域	离散 ($k=1,2,\ldots$)	离散 ($t=1,2,\ldots$)	连续 ($t \in \mathbb{R}$)
空间域	离散 (晶格)	连续 ($X_t \in \mathbb{R}$)	离散 (晶格)
步长分布	伯努利 ($\pm a$)	高斯 ($N(0, \sigma^2)$)	固定 (例如 $+1$)
步长时间	固定间隔 ($\tau$)	固定间隔 ($\tau=1$)	随机 (指数分布)
核心统计工具	二项分布 -> 高斯 (CLT)	特征函数	生存概率
极限分布	高斯分布 (位置)	高斯分布 (位置)	指数分布 (等待时间)

1. 复习：简单随机游走（SRW）及其连续极限¶

为了更好地理解本讲的内容，我们首先回顾上一讲的核心模型——简单随机游走（Simple Random Walk, SRW），并阐明其与本讲内容的内在联系。教授在黑板上的板书清晰地勾勒出了这一过渡的数学脉络。

离散SRW模型的核心结论¶

在一个一维坐标系上，一个粒子在每个离散的时间步长 $\tau$ 内，以概率 $p$ 向右移动距离 $a$，以概率 $q=1-p$ 向左移动距离 $a$。经过 $k$ 步（总时间 $t_k = k\tau$）后，我们得到以下关键统计特性：

平均位移：粒子的期望位置随时间线性增长，其速度由左右跳跃的概率差决定。

\[ \langle X_k \rangle = v t_k, \quad \text{其中速度 } v = \frac{(p-q)a}{\tau} \]

位置概率：粒子在 $k$ 步后位于 $na$ 处的概率由二项分布描述。若向右跳了 $k_+$ 步，向左跳了 $k_-$ 步，则 $k = k_+ + k_-$ 且 $n = k_+ - k_-$。

$$ \text{Prob}{X_k = na} = \binom{k}{k_+} p^{k_+} (1-p)^{k_-} $$

方差与扩散：位置的方差同样随时间线性增长，这正是扩散过程的标志性特征。

$$ \text{Var}[X_k] = 2D t_k, \quad \text{其中扩散系数 } D = \frac{2pqa^2}{\tau} $$

物理意义: 这两个简单的公式揭示了随机过程从微观到宏观的两个基本特征。

漂移（Drift）: 平均位移 $\langle X_k \rangle \propto t_k$ 描述了系统整体的定向运动趋势。这个趋势由微观上的不对称性（$p \neq q$）决定。就像一阵微弱但持续的风，虽然每片落叶的轨迹曲折随机，但整个叶群会朝着风的方向缓慢漂移。
扩散（Diffusion）: 方差 $\text{Var}[X_k] \propto t_k$ 则描述了系统在平均趋势周围的“模糊”或“不确定性”的增长。这是由微观随机性（$p$ 和 $q$ 都不为 $0$）的累积效应造成的。即使风是匀速的（$p=q$，无漂移），叶子也会因为空气的随机扰动而散开，其散开的范围（标准差 $\sigma \propto \sqrt{t_k}$）随时间增长。方差与时间的一次方关系是扩散过程的“指纹”，它告诉我们，不确定性是通过大量独立的随机事件累积起来的。

我们看到，尽管每一步都是完全随机的，但大量步骤的集体行为却呈现出规律性——平均位移的线性增长和方差的线性增长（即扩散）。

然而，真实世界中的许多过程，例如细胞内分子马达的运动、化学反应的发生，其时间演化是连续的。本讲的目标，就是将我们从离散的世界观平滑地过渡到连续的世界观。我们将看到，当观察尺度远大于单次跳跃的步长和时间间隔时，离散的二项分布如何“涌现”出连续的、普适的高斯分布。当我们考虑大量、微小且频繁的步进时，离散的格点模型便过渡到了一个连续的空间和时间模型。这一过程的核心，正是统计物理学中最深刻的思想之一——中心极限定理（Central Limit Theorem, CLT）。Frey教授进一步引导我们思考：为什么高斯分布如此特殊？为什么无论微观细节如何，宏观上我们总能看到它？这背后隐藏着一种被称为“吸引子”（Attractor）和“普适性”（Universality）的深刻思想，而参考论文中提到的重整化群（Renormalization Group, RG）方法，则为我们理解这种普适性提供了强大的理论武器。

2. 高斯分布：一个普适的吸引子¶

当步数$k$非常大时，描述粒子位置的二项分布可以被一个高斯（正态）分布极好地近似。这正是中心极限定理（Central Limit Theorem, CLT）的核心内容。

\[ \binom{k}{k_+} p^{k_+} (1-p)^{k_-} \approx \frac{1}{\sqrt{2\pi \text{Var}[n]}} \exp\left[-\frac{(n - \langle n \rangle)^2}{2 \text{Var}[n]}\right] \]

其中，$\langle n \rangle = k(p-q)$，$\text{Var}[n] = 4kpq$

$p(x,t)$ 是在时间 $t$、位置 $x$ 处找到行走者的概率密度。

分布的峰值以速度 $v$ 移动，这对应于我们之前讨论的漂移。

分布的宽度由标准差 $σ_t=\sqrt{2Dt}$ 决定，它随着时间的平方根增长。这表明粒子正在通过扩散向外散开，正如幻灯片中的图像所示：随着时间的推移，蓝色曲线变得越来越宽、越来越平坦。

课堂的PPT指出，高斯随机游走是所有具有弱局部关联的随机游走的"普适吸引子"（universal attractor）。这个概念源于动力系统和统计物理学，其物理意义远比一个单纯的数学近似要深刻。这个近似的物理前提是，我们的观察尺度（最终位移 $x$）远大于单步步长 $a$，且总时间$t$ 远大于单步时间 $τ$。正是在这种宏观视角下，微观的离散性变得不再重要，连续的、平滑的高斯分布才作为一种有效的宏观描述而涌现。

它意味着，在长时间、大尺度下，随机过程的宏观统计行为（最终呈现高斯分布）并不依赖于其微观细节（例如，单步的跳跃是遵循伯努利分布、均匀分布还是其他分布）。只要单步的随机变量满足某些基本条件（例如具有有限的方差），它们大量累加后的结果总会被"吸引"到同一个终点——高斯分布。

CLT的直观解释是：大量独立同分布的随机变量（在这里是我们的每一步）之和，其分布会趋向于一个高斯分布（也称正态分布），无论单步的分布具体是什么样的（只要其方差是有限的）。因此，中心极限定理因此成为了连接离散微观世界与连续宏观世界的桥梁，并揭示了自然界中一个深刻的原理：普适性（universality）。正是这种普适性，使得我们能够忽略微观细节的复杂性，抓住支配系统宏观行为的共同规律。这一思想也为我们后续理解更广义的重整化群理论埋下了伏笔。

2.1 模型定义¶

高斯随机游走（GRW）描述的是空间连续、但时间以固定步长推进的过程，定义为一个随机变量序列$X_t$，其演化规则如下：

\[ X_t = X_{t-1} + \xi_t \]

其中，$X_t$是$t$时刻的位置，而$\xi_t$是在该时刻的随机位移。与SRW不同，$\xi_t$是一个连续随机变量，它从一个高斯分布$W(\xi_t)$中抽取，该分布的均值为0，方差为$\sigma_\xi^2$ 。

\[ W(\xi_t) = \frac{1}{\sqrt{2\pi\sigma_\xi^2}} \exp\left(-\frac{\xi_t^2}{2\sigma_\xi^2}\right) \]

假设从$X_0 = 0$出发，经过$t$步后，总位移是所有独立同分布（i.i.d.）的单步位移之和：

\[ X_t = \sum_{t'=1}^{t} \xi_{t'} \]

2.2 统计性质的直接计算¶

我们可以直接利用期望和方差的线性性质来计算$X_t$的统计特性：

平均位移：由于每一步的平均位移$\langle \xi_{t'} \rangle = 0$，总位移的平均值也为0。

\[ \langle X_t \rangle = \left\langle \sum_{t'=1}^{t} \xi_{t'} \right\rangle = \sum_{t'=1}^{t} \langle \xi_{t'} \rangle = 0 \]

方差：由于每一步的位移$\xi_{t'}$是相互独立的，总位移的方差等于各步方差之和。如果每一步的方差都相同，记为$\sigma_\xi^2$，那么：

\[ \langle X_t^2 \rangle = \text{Var}[X_t] = \left\langle \left(\sum_{t'=1}^{t} \xi_{t'}\right) \left(\sum_{t''=1}^{t} \xi_{t''}\right) \right\rangle = \sum_{t'=1}^{t} \sum_{t''=1}^{t} \langle \xi_{t'} \xi_{t''} \rangle \]

因为$\langle \xi_{t'} \xi_{t''} \rangle = \delta_{t't''} \sigma_\xi^2$（仅当$t'=t''$时不为零），所以：

\[ \langle X_t^2 \rangle = \sum_{t'=1}^{t} \langle \xi_{t'}^2 \rangle = \sum_{t'=1}^{t} \sigma_\xi^2 = t \sigma_\xi^2 \]

这再次验证了方差随时间线性增长的扩散特性。

2.3 特征函数：处理随机变量和的利器¶

虽然直接计算均值和方差很简单，但要获得完整的概率分布函数$p(x,t)$则更为复杂。对于处理独立随机变量求和的问题，特征函数（characteristic function）是一个极其强大的数学工具。

2.3.1 定义与作用¶

一个随机变量$X$的特征函数定义为其$e^{isX}$的期望值：

\[ \chi_X(s) = \langle e^{isX} \rangle = \int_{-\infty}^{\infty} e^{isx} p(x) dx \]

其中$i$是虚数单位，$s$是实数变量。从定义可以看出，特征函数本质上是概率密度函数（PDF）的傅里叶变换。它之所以如此重要，主要基于以下几个关键性质：

唯一性：一个概率分布被其特征函数唯一确定。如果两个随机变量的特征函数相同，那么它们的概率分布也必然相同。
求和性质：这是其最核心的优势。对于两个独立的随机变量$X$和$Y$，它们的和$Z=X+Y$的特征函数等于它们各自特征函数的乘积：$\chi_Z(s) = \chi_X(s) \chi_Y(s)$ 。

这一性质将一个在实空间中复杂的卷积运算（$p_Z(z) = \int p_X(x)p_Y(z-x)dx$）转换为了在傅里叶空间中简单的乘法运算，极大地简化了分析过程。

2.3.2 GRW的特征函数推导¶

现在，我们运用特征函数来推导$X_t$的完整概率分布，这完整地复现了教授在黑板上的演算过程。

单步的特征函数：首先计算单步高斯位移$\xi_t$的特征函数$\chi_{\xi_t}(s)$。

\[ \chi_{\xi_t}(s) = \langle e^{is\xi_t} \rangle = \int_{-\infty}^{\infty} e^{is\xi} \frac{1}{\sqrt{2\pi\sigma_\xi^2}} e^{-\frac{\xi^2}{2\sigma_\xi^2}} d\xi = e^{-\frac{1}{2}s^2\sigma_\xi^2} \]

这是一个标准的高斯积分结果，表明高斯分布的傅里叶变换仍然是高斯形式。

$t$步和的特征函数：由于$X_t = \sum_{t'=1}^{t} \xi_{t'}$是$t$个独立随机变量的和，其特征函数$\chi_{X_t}(s)$是所有单步特征函数的乘积。

\[ \chi_{X_t}(s) = \left\langle e^{is \sum_{t'=1}^{t} \xi_{t'}} \right\rangle = \left\langle \prod_{t'=1}^{t} e^{is\xi_{t'}} \right\rangle \]

由于各步独立，期望的乘积等于乘积的期望：

\[ \chi_{X_t}(s) = \prod_{t'=1}^{t} \langle e^{is\xi_{t'}} \rangle = \prod_{t'=1}^{t} \chi_{\xi_{t'}}(s) \]

代入单步的结果，得到：

\[ \chi_{X_t}(s) = \prod_{t'=1}^{t} e^{-\frac{1}{2}s^2\sigma_\xi^2} = e^{-\frac{1}{2}s^2 \sum_{t'=1}^{t} \sigma_\xi^2} = e^{-\frac{1}{2}s^2 (t\sigma_\xi^2)} \]

得到概率分布函数：我们将最终结果与单步的特征函数形式进行比较。我们发现$\chi_{X_t}(s)$正是一个均值为0、方差为$\sigma_{X_t}^2 = t\sigma_\xi^2$的高斯分布所对应的特征函数。根据特征函数的唯一性，我们可以断定$X_t$也服从高斯分布。通过逆傅里叶变换，即可得到其概率密度函数：

\[ p(x,t) = \frac{1}{\sqrt{2\pi\sigma_{X_t}^2}} \exp\left(-\frac{x^2}{2\sigma_{X_t}^2}\right) \]

这个推导完美地展示了特征函数的威力：一个涉及$t$次卷积的复杂问题，通过转换到傅里叶空间，变成了简单的指数乘法，最终轻松得到解析结果。

为了直观地理解GRW的特性，我们可以通过Python代码进行模拟。下面的代码模拟了多条GRW轨迹，并展示了在不同时刻粒子位置的分布情况。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# --- Parameter settings ---
num_walkers = 5000  # Number of simulated particles
num_steps = 100     # Total number of steps
sigma_xi = 1.0      # Standard deviation of single-step displacement (σ_ξ)
plot_times = [10, 30, 100]  # Time points at which to plot the distribution

# --- Simulation process ---
# Generate random displacements for all steps, shape is (num_walkers, num_steps)
# Each step is sampled from N(0, sigma_xi^2)
steps = np.random.normal(loc=0.0, scale=sigma_xi, size=(num_walkers, num_steps))

# Calculate the position of each walker at each step (cumulative sum)
# positions has the same shape as (num_walkers, num_steps)
positions = np.cumsum(steps, axis=1)

# --- Visualization of results ---
plt.figure(figsize=(12, 6))
plt.suptitle('Gaussian Random Walk Simulation', fontsize=16)

# Plot some sample trajectories
plt.subplot(1, 2, 1)
for i in range(5): # Only plot 5 trajectories as examples
    plt.plot(range(1, num_steps + 1), positions[i, :], alpha=0.7)
plt.title('Sample Trajectories')
plt.xlabel('Time Step (t)')
plt.ylabel('Position (X_t)')
plt.grid(True)

# Plot position distributions at specified time points
plt.subplot(1, 2, 2)
for t in plot_times:
    # Theoretical variance
    variance_t = t * sigma_xi**2
    std_dev_t = np.sqrt(variance_t)

    # Plot histogram of simulation data
    plt.hist(positions[:, t-1], bins=50, density=True, alpha=0.6, label=f't = {t} (Sim)')

    # Plot theoretical Gaussian distribution curve
    x = np.linspace(-4 * std_dev_t, 4 * std_dev_t, 200)
    pdf = norm.pdf(x, loc=0, scale=std_dev_t)
    plt.plot(x, pdf, label=f't = {t} (Theory)')

plt.title('Position Distribution at Different Times')
plt.xlabel('Position (x)')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)

plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

模拟结果清晰地显示：随着时间$t$的增加，粒子位置的分布范围（方差）不断扩大，但其分布形状始终保持为高斯分布，这与我们的理论推导完全一致。

3.0 概念深化：普适性、标度与重整化群思想¶

在课堂上，教授在推导出高斯分布后，提及了“RG Theory”和Ariel Amir的一篇论文。这是一个非常关键但容易引起困惑的提示，因为它将一个概率论问题与现代物理学中最深刻的思想之一——重整化群（Renormalization Group, RG）——联系了起来。

由于没有讲义，教授只提及了大概的名字和作者，比较相符的文献大概是这篇：

Amir A. An elementary renormalization-group approach to the generalized central limit theorem and extreme value distributions[J]. Journal of Statistical Mechanics: Theory and Experiment, 2020, 2020(1): 013214.

3.1 标准中心极限定理的局限¶

首先需要明确，我们之前讨论的中心极限定理及其导出的高斯吸引子，其成立有一个前提：单步随机变量的方差必须是有限的。然而，在物理世界中，存在许多“重尾”（heavy-tailed）分布，它们的方差是无限的。例如，在某些玻璃态物质或金融市场中，极端事件（非常大的涨落）发生的概率远高于高斯分布的预测。对于这类系统，大量随机变量求和后的极限分布将不再是高斯分布。这就引出了一个问题：是否存在一个更普适的理论框架，能够统一描述所有这些情况？

3.2 重整化群的视角¶

重整化群理论最初是为了解决量子场论中的发散问题而发展的，但其核心思想已渗透到物理学的各个领域，尤其是在统计物理的相变理论中。

RG的核心思想：粗粒化与标度变换：RG的本质是一种系统性的“粗粒化”（coarse-graining）方法。想象一个由微观自旋构成的磁铁系统。我们可以将一小组（例如2x2）的自旋看作一个整体，用一个“等效”的块自旋来描述它们的平均行为。通过这种方式，我们忽略了微观细节，得到了一个在更大尺度上的、变量更少的新系统。然后，我们对这个新系统重复同样的操作。这个不断“放大”观察尺度、并重新调整参数以保持理论形式不变的过程，就是RG变换。
不动点与普适性：在反复进行RG变换的过程中，系统的参数会沿着某个轨迹“流动”。这个流动的终点被称为“不动点”（fixed point）。不动点所描述的系统具有标度不变性（scale invariance），即在不同尺度下看起来是自相似的。一个不动点以及所有能够流向它的初始系统，共同构成一个普适类（universality class）。同一普适类中的系统，尽管微观细节千差万别，但在宏观临界行为上表现出完全相同的性质（由相同的一组临界指数描述）。

3.3 将RG思想应用于随机游走¶

Ariel Amir的论文提供了一个绝佳的视角，将RG思想与中心极限定理联系起来。

随机变量求和即粗粒化：将$n$个独立同分布（i.i.d.）的随机变量$\xi_i$相加得到新的随机变量$S_n = \sum_{i=1}^n \xi_i$，这个过程本身就可以被看作是一次RG中的粗粒化操作。我们从$n$个微观变量出发，得到了一个描述更大尺度行为的宏观变量$S_n$。在RG的粗粒化之后，通常需要一步标度变换来将新系统与原系统进行比较。在随机游走问题中，这对应于对总位移$S_n$进行标准化处理，例如除以一个因子$\sqrt{n}$（对于方差有限的情况）。我们发现，经过$S_n / \sqrt{n}$这个变换后，分布的形式趋于稳定（高斯分布），这正体现了系统在变换下的自相似性（self-similarity）。
稳定分布即不动点：我们寻找的是求和操作下的极限分布。一个分布如果经过求和（并进行适当的平移和缩放）后，其分布形式保持不变，则称之为稳定分布（stable distribution）。在RG的语言中，这些稳定分布恰好就是求和这个RG变换的不动点。
中心极限定理的RG诠释：现在我们可以重新诠释CLT：对于所有初始分布方差有限的随机变量（这定义了一个巨大的“吸引盆”），在求和（粗粒化）这一RG流的作用下，它们都会被吸引到同一个、也是唯一一个不动点——高斯分布。初始分布的其它细节（如偏度、峰度等）在RG的语言中被称为“非相关算子”（irrelevant operators），它们在不断的粗粒化过程中被逐渐“抹平”，对最终的宏观行为没有影响。
广义中心极限定理（GCLT）：当初始分布的方差无限时（例如重尾分布），系统就不再处于高斯不动点的吸引盆内。此时，RG流会将它们带到其它的不动点。这些非高斯的稳定分布就是所谓的列维稳定分布（Lévy stable distributions）。与高斯分布不同，列维分布通常具有‘重尾’（heavy tails），意味着发生极端大跳跃的概率远高于高斯分布的预测，它们的方差甚至可能是无限的。Amir的论文正是用这种RG思想，以一种统一而优美的方式推导出了包括高斯分布和列维分布在内的所有稳定分布形式。

因此，教授提及RG理论，是为了揭示一个更深层次的图景：中心极限定理并非一个孤立的概率论结论，而是物理学中关于标度与普适性的宏大理论（RG）在一个具体问题上的体现。它告诉我们，高斯分布的无处不在，源于它在随机变量求和这一基本物理操作下所具有的独特的稳定性。

4.0 泊松过程：引入随机时间¶

到目前为止，我们讨论的模型中，时间都是以固定的、确定性的节拍向前推进的。然而，在自然界的许多过程中，事件的发生本身就是随机的。例如，放射性原子核的衰变、细胞内分子马达的运动等。泊松过程正是描述这类事件在时间上随机分布的基本模型。

4.1 动机：从“时钟”步到随机事件¶

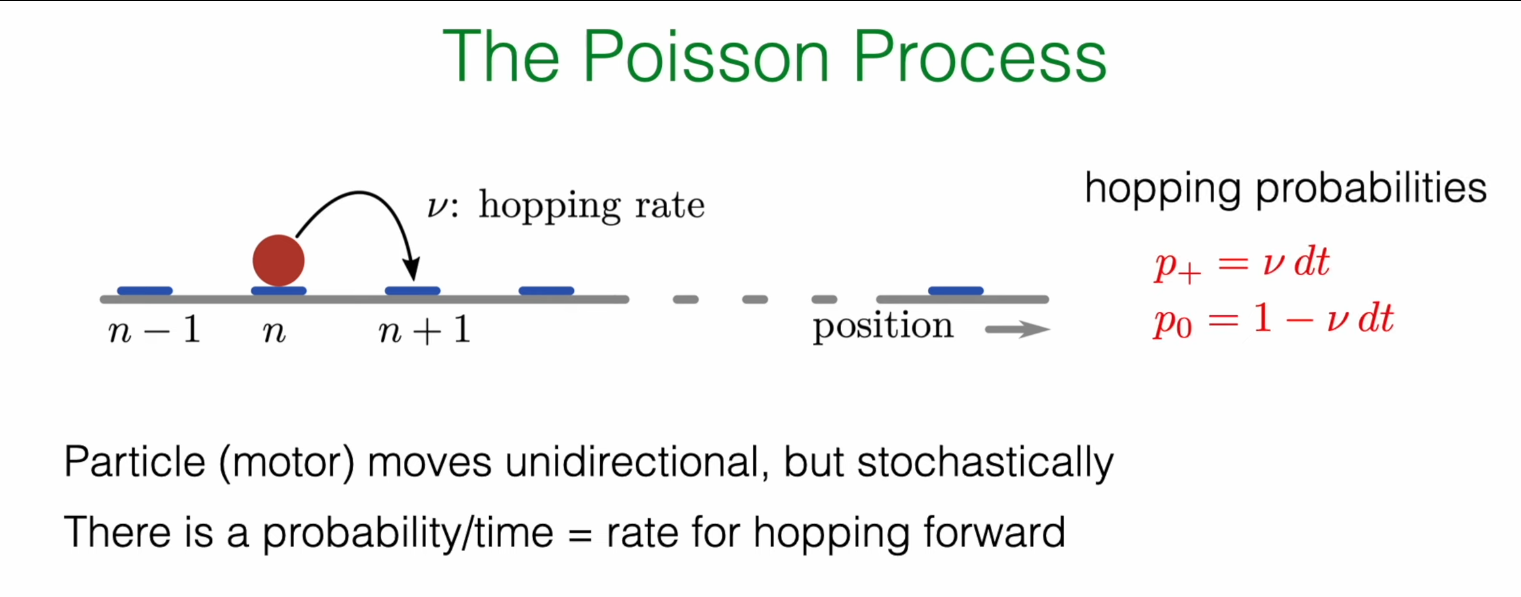
SRW和GRW模型中的粒子像一个上了发条的钟，每隔一个固定的时间$\tau$就移动一步。现在我们考虑一种新的情景：粒子在任何一个微小的时间间隔$dt$内，都有一个固定的概率向前跳一步。这个单位时间内的跳跃概率，我们称之为跳跃速率（hopping rate），记为$r$（或幻灯片中的$\nu$）。

在$dt$时间内向前跳一步的概率：$P_+ = r \cdot dt$
在$dt$时间内不动的概率：$P_0 = 1 - r \cdot dt$

这里的核心假设是$r$是一个常数，不随时间改变。

4.2 物理实例：驱动蛋白分子马达¶

课堂上展示的驱动蛋白（Kinesin）是一个绝佳的物理实例。驱动蛋白是一种分子马达，它沿着细胞内的微管“行走”，负责运输各种细胞器和囊泡。它的运动是单向的，但每一步的发生时刻是随机的。

步长：驱动蛋白的每一步大小约为 8 nm，这恰好是微管上一个微管蛋白二聚体的长度。
能量来源：每走一步，驱动蛋白需要水解一个ATP分子来提供能量。因此，其步进速率与ATP水解速率紧密耦合，通常是1:1的关系。
速率：在生理条件下，驱动蛋白的行走速率约为每秒几十到上百步。例如，实验测得的ATP水解速率可达约$50-100 \text{ s}^{-1}$ 。这使得我们之前定义的抽象跳跃速率变得非常具体：对于驱动蛋白，$r \approx 100 \text{ s}^{-1}$。

4.3 推导等待时间分布¶

泊松过程的第一个核心问题是：从一个事件发生后，需要等待多长时间，下一个事件才会发生？这个问题可以通过推导等待时间分布来回答。

4.3.1 生存概率的概念¶

我们引入一个关键量：生存概率（survival probability）$S(t) = \text{Prob}\{T > t\}$，它表示直到$t$时刻，我们关心的事件（例如，一次跳跃）还未发生的概率。这里的$T$是等待时间这个随机变量。根据定义，生存函数与累积分布函数（CDF）$F(t) = \text{Prob}\{T \le t\}$的关系是$S(t) = 1 - F(t)$。

4.3.2 从差分到微分方程¶

现在我们来推导$S(t)$的演化方程，这同样是黑板上的核心推导。

考虑$t+dt$时刻的生存概率$S(t+dt)$。系统要“存活”到$t+dt$时刻，必须满足两个独立条件：

它已经存活到了$t$时刻（概率为$S(t)$）。
并且，在接下来的$[t, t+dt]$这个微小时间段内，没有发生跳跃（概率为$1 - r dt$）。

因此，

\[ S(t+dt) = S(t) \cdot (1 - r dt) \]

对上式进行整理：

\[ \frac{S(t+dt) - S(t)}{dt} = -r S(t) \]

当$dt \to 0$时，左边就是$S(t)$的导数，我们得到一个一阶常微分方程：

\[ \frac{dS(t)}{dt} = -r S(t) \]

4.3.3 指数分布¶

这个微分方程的解非常简单。我们知道初始条件是$S(0)=1$（在$t=0$时刻，事件肯定还未发生）。求解该方程得到：

\[ S(t) = e^{-rt} \]

我们得到了生存概率函数。而等待时间的概率密度函数$p(t)$可以通过对$F(t) = 1 - S(t)$求导得到，即$p(t) = -dS/dt$：

\[ p(t) = r e^{-rt} \]

这就是指数分布。它描述了在事件发生速率恒定的情况下，两次连续事件之间的等待时间的分布。

4.4 泊松过程的性质¶

从指数分布可以导出泊松过程的一些重要性质：

平均等待时间：$\langle T \rangle = \int_0^\infty t \cdot p(t) dt = 1/r$。这符合直觉：速率越高，平均等待时间越短。
等待时间方差：$\text{Var} = 1/r^2$。
无记忆性（Memoryless Property）：这是指数分布最独特的性质。它指的是，未来事件发生的概率与过去等待了多久无关。数学上表示为$\text{Prob}(T > t+s | T > t) = \text{Prob}(T > s)$。也就是说，如果我们已经等了$t$秒，驱动蛋白还没动，那么它在接下来$s$秒内依然不动的概率，和一个刚开始等待的驱动蛋白在$s$秒内不动的概率是完全一样的。这个系统的“历史”被遗忘了。这个性质直接源于我们最初的物理假设——跳跃速率$r$是一个不随时间改变的常数。

4.5 事件计数：泊松分布¶

除了等待时间，泊松过程的另一个核心问题是：“在给定的时间窗口 $T$ 内，恰好发生 $k$ 次事件的概率是多少？”其答案由泊松分布给出：

\[ P(k; T) = \frac{(\nu T)^k}{k!} e^{-\nu T} \]

其中，$\lambda = \nu T$ 是在该时间窗口内期望发生的平均事件数。这个分布与指数分布共同构成了对泊松过程的完整描述：指数分布描述了“事件之间要等多久”，而泊松分布则描述了“一段时间内能发生多少事”。

5.0 模拟：Gillespie算法¶

该算法的详细细节将在下一个讲座中介绍。

上一节的理论推导不仅给出了泊松过程的统计性质，也为我们提供了一种精确、高效的计算机模拟方法，即Gillespie算法（或称随机模拟算法，SSA）。传统的模拟方法可能会将时间离散化成许多微小的$dt$，然后在每个$dt$内根据概率$r dt$来决定是否发生事件。这种方法不仅计算效率低下，而且是近似的。

Gillespie算法的精髓在于，它利用我们已经推导出的解析结果，直接回答两个问题：

下一个事件将在何时发生？ 答案是：等待时间$\Delta t$从指数分布$p(t) = re^{-rt}$中抽取。
将发生什么事件？ （在有多种可能事件时）答案是：根据各事件的相对速率来决定。例如，如果一个粒子既可以以速率$\nu_f$向前跳，也可以以速率$\nu_b$向后跳，那么总速率为$\nu_{total} = \nu_f + \nu_b$。在确定了下一步发生后，它向前跳的概率为$\nu_f / \nu_{total}$，向后跳的概率为$\nu_b / \nu_{total}$。通过这种方式，Gillespie算法可以精确模拟任意复杂的随机反应网络。

对于我们目前讨论的简单单向跳跃过程，第二步是确定的（只会向前跳）。因此，算法的核心就是不断地从指数分布中生成下一个等待时间。

下面的Python代码实现了Gillespie算法，用于模拟一个简单的单向泊松过程。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import poisson, expon

# --- Parameter settings ---
r = 2.0                # Average event rate
T_max = 10.0             # Total simulation time for trajectories
num_trajectories = 10    # [Modification] Increase the number of displayed trajectories to 10
num_simulations = 20000  # Number of simulations for statistical distribution

# --- Create canvas ---
fig = plt.figure(figsize=(14, 10))
ax_traj = plt.subplot2grid((2, 2), (0, 0), colspan=2)
ax_count = plt.subplot2grid((2, 2), (1, 0))
ax_wait = plt.subplot2grid((2, 2), (1, 1))

fig.suptitle(f'Poisson Process: Trajectories and Underlying Distributions (Rate r = {r})', fontsize=16)

# --- 1. Simulate and plot several trajectories (top plot) ---
all_waiting_times = [] 
for i in range(num_trajectories):
    t = 0.0
    x = 0
    times = [t]
    positions = [x]

    while t < T_max:
        delta_t = np.random.exponential(scale=1.0/r)
        all_waiting_times.append(delta_t)

        t += delta_t
        if t < T_max:
            x += 1
            times.append(t)
            positions.append(x)

    # To make the graph clear, only add labels for the first few trajectories
    if i < 3:
        ax_traj.step(times, positions, where='post', label=f'Sample Trajectory {i+1}')
    else:
        ax_traj.step(times, positions, where='post', alpha=0.6) # Make subsequent trajectories semi-transparent

# Plot theoretical mean line
t_theory = np.linspace(0, T_max, 100)
mean_theory = r * t_theory
ax_traj.plot(t_theory, mean_theory, 'k--', linewidth=2.5, label=f'Theoretical Mean N(t) = {r}*t')
ax_traj.set_title(f'Sample Trajectories of a Poisson Process ({num_trajectories} shown)')
ax_traj.set_xlabel('Time (t)')
ax_traj.set_ylabel('Number of Events (N(t))')
ax_traj.grid(True, linestyle='--', alpha=0.6)
ax_traj.legend()


# --- 2. Plot event count distribution (bottom left plot) ---
event_counts_at_Tmax = np.random.poisson(lam=r * T_max, size=num_simulations)
k_values = np.arange(event_counts_at_Tmax.min(), event_counts_at_Tmax.max() + 1)
ax_count.hist(event_counts_at_Tmax, bins=np.arange(k_values.min(), k_values.max() + 2) - 0.5, density=True, alpha=0.7, label='Simulation')

poisson_pmf_theory = poisson.pmf(k=k_values, mu=r * T_max)
ax_count.plot(k_values, poisson_pmf_theory, 'ro-', label='Theory (Poisson)')
ax_count.set_title(f'Event Count Distribution at T={T_max}')
ax_count.set_xlabel(f'Number of Events (k)')
ax_count.set_ylabel('Probability')
ax_count.set_xticks(k_values[::2])
ax_count.legend()
ax_count.grid(True, linestyle='--', alpha=0.6)


# --- 3. Plot waiting time distribution (bottom right plot) ---
additional_waits = np.random.exponential(scale=1.0/r, size=num_simulations)
all_waiting_times.extend(additional_waits)

ax_wait.hist(all_waiting_times, bins=50, density=True, alpha=0.7, label='Simulation')

t_values_exp = np.linspace(0, max(all_waiting_times), 200)
expon_pdf_theory = expon.pdf(t_values_exp, scale=1.0/r)
ax_wait.plot(t_values_exp, expon_pdf_theory, 'r-', linewidth=2, label='Theory (Exponential)')
ax_wait.set_title('Waiting Time Distribution')
ax_wait.set_xlabel('Time between events (Δt)')
ax_wait.set_ylabel('Probability Density')
ax_wait.legend()
ax_wait.grid(True, linestyle='--', alpha=0.6)


# --- Display final image ---
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

可以看到，没有任何两条轨迹是完全一样的，它们的跳跃时间点各不相同，最终在$t=10$秒时的位置也各不相同。然而，尽管它们充满随机，但所有轨迹都围绕着黑色的理论平均线 $N(t) = 2.0 \cdot t$ 上下波动。单个过程是不可预测的，但其长期行为会遵循一个平均趋势。

左下图 (事件计数分布)：这幅图从统计学角度揭示了过程的确定性规律。它统计了成千上万次模拟在$t=10$秒这个精确时刻的最终位置，并绘制成直方图。我们会发现，尽管单次实验的结果是随机的，但大量实验的结果分布却呈现出一个非常规则的钟形。更重要的是，这个由模拟数据（蓝色）构成的分布，与理论上的泊松分布（红色圆点线）重合。固定时间点，系统所处状态的概率是可以被精确预测的。

右下图 (等待时间分布)：这幅图深入到过程的微观动力学。它将所有轨迹中每一次“跳跃”之间的时间间隔（即顶部图中每个阶梯的“水平长度”）收集起来，绘制成其概率分布。结果显示，绝大多数等待时间都很短，而长等待时间则非常罕见，其概率呈指数衰减。这个模拟结果（蓝色）同样与理论上的指数分布（红线）吻合。驱动整个过程演化的“引擎”——事件发生的等待时间——本身就是一个遵循严格概率规律的随机变量。

总结¶

本讲座带领我们完成了从离散到连续随机过程的两个关键跨越，深化了我们对随机现象的理解：

从离散空间到连续空间：我们看到，简单随机游走在宏观极限下趋向于高斯分布。这一过程不仅可以用中心极限定理来描述，更可以从重整化群的深刻思想中得到诠释，即高斯分布是求和操作下的一个普适不动点。在这一过程中，特征函数作为分析工具，展示了其在处理独立随机变量和问题上的巨大威力。
从离散时间到连续时间：通过引入一个恒定的事件发生速率$r$，我们构建了泊松过程模型。其核心在于，两次事件间的等待时间服从指数分布，并具有独特的无记忆性。生存概率的分析方法，通过建立并求解微分方程，成为推导这一结果的关键。

贯穿本讲的核心主题是，如何从简单的、微观的物理假设（如单步跳跃分布、恒定事件率）出发，推导出具有普适性的、宏观的统计规律。

一个自然而然的步骤是将这两个思想结合起来：研究一个在连续空间中、其事件发生在连续随机时间上的过程。这将直接引导我们进入布朗运动的领域，以及描述它的数学语言——朗之万方程（Langevin Equation）和福克-普朗克方程（Fokker-Planck Equation），这些将是后续课程中探讨的核心内容。

特性	简单随机游走 (SRW)	高斯随机游走 (GRW)	泊松过程 (Poisson Process)
时间域	离散 (\(k=1,2,\ldots\))	离散 (\(t=1,2,\ldots\))	连续 (\(t \in \mathbb{R}\))
空间域	离散 (晶格)	连续 (\(X_t \in \mathbb{R}\))	离散 (晶格)
步长分布	伯努利 (\(\pm a\))	高斯 (\(N(0, \sigma^2)\))	固定 (例如 \(+1\))
步长时间	固定间隔 (\(\tau\))	固定间隔 (\(\tau=1\))	随机 (指数分布)
核心统计工具	二项分布 -> 高斯 (CLT)	特征函数	生存概率
极限分布	高斯分布 (位置)	高斯分布 (位置)	指数分布 (等待时间)